Momentum Conservation and Transfer
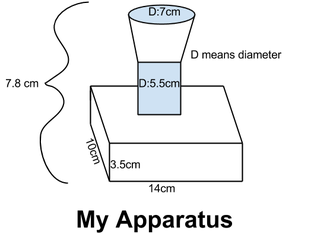
Part 1. A bare egg dropped from one meter would have -.251kgm/s of momentum at the moment before impact. To get the momentum of the moment before impact of the egg, I first had to find time using the equation change of y=(1/2)a(t^2)+Vot, which change of y is the amount of change in the vertical direction, the (1/2) is a constant that never changes, the a is the acceleration of the egg(-9.8m/s^2), t^2 is time squared, Vo is the initial velocity of the egg(0m/s) and t is just time. So then you plug in all the numbers and solve for t. Which in order to find t you need to use the quadratic formula. So, then t is equal to .45 seconds(s). I had to find the overall velocity with the equation of V=Vo+at and plugged in the numbers again to be V=(0m/s)+(-9.8m/s^2)(.45s), and found that V is -4.41m/s. After that I used V in the equation of P=mV, where P is momentum, m is mass(.057kg), and V is veloctiy. After plugging in numbers to that equation, it would be P=(.057kg)(-4.41m/s). So, P equals -.251 kgm/s. If that is the eggs momentum, the floor would exert .251ns of impulse to stop the egg. I found how much force the floor would exert of impulse to stop the egg by using the equation to find the difference between the two answers(P=0 and P=-.251), so the change in P would be 0-(-.251)=.251. And in out experiment, the apparatus exerted the impulse for .04s(analysis of our video.) And to find how much time our apparatus exerted of impulse for, I took how many frames were taken of our video while the egg was touching the apparatus and divided it by how many frames were actually being taken by the camra. Which was 240 frames per second. By doing that I got .04seconds, which is how long the apparatus extered an impulse on our egg. Therefore, our apparatus exerted 6.275n of average force. I found how many newtons our apparatus exerted of an average force. I used the equation F(change in t)=m(change in V). Which F is the force, change in t is the change in time that it took, m is the mass, and change in V is the change in velocity. So, I plugged in all of the numbers which was F(.04s)=(.057kg)(4.41m/s) and found that F=6.275 newtons(n).
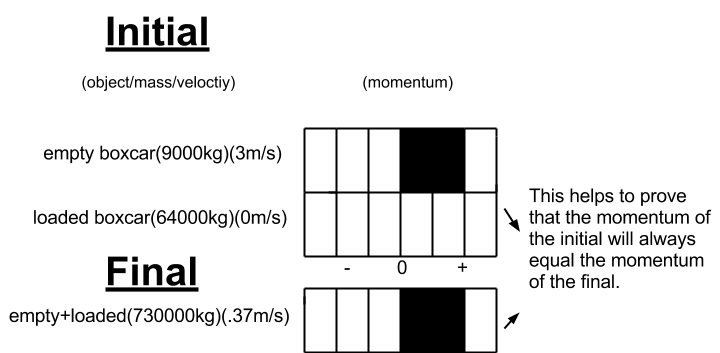
Part 2. To find the momenntum of a 9000kg loaded boxcar going 3m/s, you used the equation P=mV. P stands for momentum, m stands for mass(9000kg) and V stands for velocity or speed(3m/s). Then after plugging those numbers in it would be P=(9000kg)(3m/s), so P=27000kgm/s. The same equation is used to find the P of a 64000kg empty boxcar and 0m/s is the velocity. So P=(64000kg)(0m/s), P of the empty boxcar is 0kgm/s. Although, a different equation is used to find the P after the two cars collide with eachother. It is P of the empty boxcar plus the P of the loaded boxcar. So, (0kgm/s)+(27000kgm/s)=P of the collision. So, 27000kgm/s=P of the collision. Now to find the exact speed of the two collided boxcars you would take the P which is equal to its masses added up(m) and the speed it is going and direction it is going(V). So, 27000kgm/s=(73000kg)(V). So to find V, you would divide 27000kgm/s by 73000kg and get V=.37m/s. Where V is the speed of the speed of the two boxcars together. 73000kg refers to the weight of both of the boxcars added together.