Projectile Motion
During a thunderstorm, a tornado lifts a car to a height of 125 meters(m) above the ground. Increasing in strength, the tornado flings the car horizontally with an initial speed of 90 meters per second(m/s).
It takes the car 5.05 seconds(s) to reach the ground. To find the time it took, I used the quadratic position formula because the xt graph is quadratic. This formula is y=(1/2)at^2+Vo(t). Then I plugged in all the numbers that I already knew, and solved for t. So, -125m is how far the car traveled in the y direction(y), the -9.8m/(s^2) is the rate the car was accelerating(a), and finally 0m/s is the initial velocity of the car(Vo). That is, -125m=(1/2)[-9.8m/(s^2)]t^2+(0m/s)t. That will equal to -125m=[-4.9m/(s^2)]t^2. And that is equal to 25.5s^2=t^2. So, finally after square rooting both sides, t=5.05seconds
The car travels 454.5meters(m) in the x direction. I found this by using the linear position graph formula, x=Vx(t) because the xt graph is a linear graph. So x is the horizontal change, 90m/s is how fast the car is moving in the x direction initially(Vx), and the time is 5.05s(t). So after you plug in all the numbers into the equation it would be x=(90m/s)(5.05s). Then x will equal 454.5m.
During a thunderstorm, a tornado lifts a car to a height of 125 meters(m) above the ground. Increasing in strength, the tornado flings the car horizontally with an initial speed of 90 meters per second(m/s).
It takes the car 5.05 seconds(s) to reach the ground. To find the time it took, I used the quadratic position formula because the xt graph is quadratic. This formula is y=(1/2)at^2+Vo(t). Then I plugged in all the numbers that I already knew, and solved for t. So, -125m is how far the car traveled in the y direction(y), the -9.8m/(s^2) is the rate the car was accelerating(a), and finally 0m/s is the initial velocity of the car(Vo). That is, -125m=(1/2)[-9.8m/(s^2)]t^2+(0m/s)t. That will equal to -125m=[-4.9m/(s^2)]t^2. And that is equal to 25.5s^2=t^2. So, finally after square rooting both sides, t=5.05seconds
The car travels 454.5meters(m) in the x direction. I found this by using the linear position graph formula, x=Vx(t) because the xt graph is a linear graph. So x is the horizontal change, 90m/s is how fast the car is moving in the x direction initially(Vx), and the time is 5.05s(t). So after you plug in all the numbers into the equation it would be x=(90m/s)(5.05s). Then x will equal 454.5m.
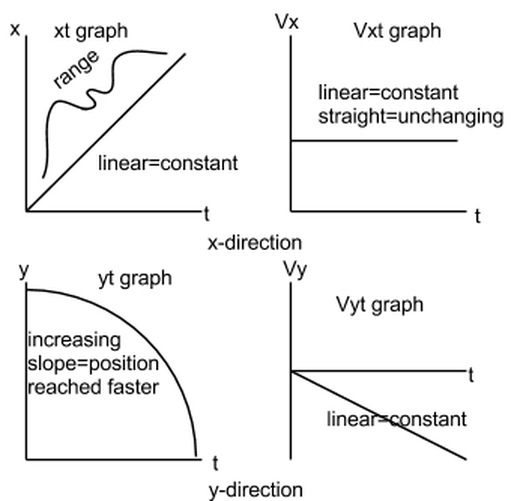
The xt graph: the range increases a constant rate.
The Vxt graph: the car moves at a constant velocity in the x-direction.
The yt graph: the fall, increasing in speed(that is why the slope steepens) and lands farther away than where is starts
The Vyt graph: the car is falling downward at an increasingly faster rate(that is why it is a constant increase)
The Vxt graph: the car moves at a constant velocity in the x-direction.
The yt graph: the fall, increasing in speed(that is why the slope steepens) and lands farther away than where is starts
The Vyt graph: the car is falling downward at an increasingly faster rate(that is why it is a constant increase)