Contact Forces
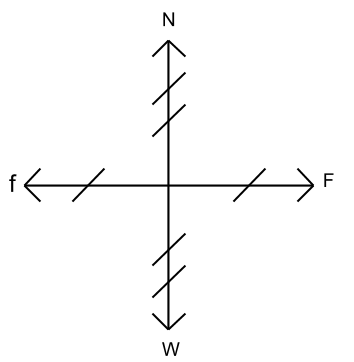
A block weighing 300newtons(n) moved at a constant speed over a horizonal surface by a force of 50n applied paralled to the surface. N is the normal force, which is the horizontal surface supporting the block vertically. W is the gravitational pull down on the block. F is the force moving the block horizontally. f is the force that is opposing the motion of the block(friction). All of the force vectors are balanced so N and W are equal, and f and F are equal. Since the N and W forces are balanced, N equals W, so because W=300n because that is the weight of the block. So that means, N=300n. There is 50n of F applied. But I only know that because it was given. I checked that they were balanced with this equation EF=ma. Where EF is the net force, which means both the forces, horizontally or vertically, added together, which in this case is F-f(f is negative because it is pushing in the opposite direction, where m means mass, and a is the acceleration. Also, because f and F and balanced, F=50n. And because friciton only acts in the horizontal direction, F is the only force affected. Also, the right side of the equation is 0N because there is no accelertion. So that means 50n-f=0 so f equals -50. But because forces can not push negatively, it is actually 50n. The coefficiant of kinetic friction was found with the equation of f=(u)(N), where f is the friction applied, u is the miu, and N is the normal force. I plugged 50n in for f because that is the amount of f applies to the block, 300n in for N because that is how much N applies on the block. Then I solved for u and got .167.
A block weighing 300newtons(n) moved at a constant speed over a horizonal surface by a force of 50n applied paralled to the surface. N is the normal force, which is the horizontal surface supporting the block vertically. W is the gravitational pull down on the block. F is the force moving the block horizontally. f is the force that is opposing the motion of the block(friction). All of the force vectors are balanced so N and W are equal, and f and F are equal. Since the N and W forces are balanced, N equals W, so because W=300n because that is the weight of the block. So that means, N=300n. There is 50n of F applied. But I only know that because it was given. I checked that they were balanced with this equation EF=ma. Where EF is the net force, which means both the forces, horizontally or vertically, added together, which in this case is F-f(f is negative because it is pushing in the opposite direction, where m means mass, and a is the acceleration. Also, because f and F and balanced, F=50n. And because friciton only acts in the horizontal direction, F is the only force affected. Also, the right side of the equation is 0N because there is no accelertion. So that means 50n-f=0 so f equals -50. But because forces can not push negatively, it is actually 50n. The coefficiant of kinetic friction was found with the equation of f=(u)(N), where f is the friction applied, u is the miu, and N is the normal force. I plugged 50n in for f because that is the amount of f applies to the block, 300n in for N because that is how much N applies on the block. Then I solved for u and got .167.